Constant Contact Angle - Boundary Condition Description
Constant Contact Angle is a boundary condition that enforces a constant contact angle for the alpha (volume fraction) field at a wall in two-phase simulations. It prescribes a fixed contact angle value \(\theta_0\) used by the alpha-contact-angle treatment to compute the wall boundary value of the phase fraction and the orientation of the interface at the contact line. Unlike Zero Gradient, which allows the interface to meet the wall at any angle, this BC ensures the prescribed angle for accurate capillary forces and interface shapes.
This boundary condition is commonly applied at open boundaries in multiphase simulations where pressure varies with height due to gravity.
It is particularly suitable for modeling hydrostatic pressure profiles in tanks, reservoirs, or environmental flows, where the pressure depends on the vertical position and the density of a specified phase.
Examples include water-air interfaces in storage tanks, outlet boundaries in stratified flows, and pressure loading on submerged surfaces.
Constant Contact Angle - Boundary Condition Understanding Constant Contact Angle
The contact angle is the angle between the liquid–vapor interface and the solid surface at the three‑phase contact line. It quantifies how a liquid wets a solid and is determined by the balance of interfacial tensions between solid–vapor, solid–liquid, and liquid–vapor interfaces.
Graphically, the contact angle can be represented as in Figure 1.
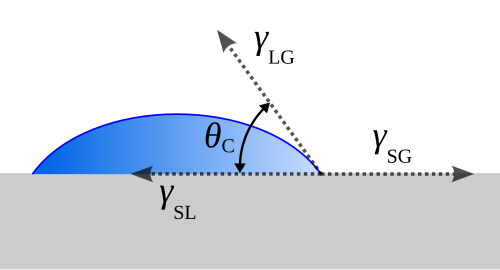
Young’s equation relates the equilibrium contact angle \(\theta_C\) to the interfacial tensions:
where :
\(\theta_0\) - contact angle \([deg]\) or \([rad]\),
\(\gamma_{SG}\) - solid-vapor interfacial tension \([\frac{N}{m}]\),
\(\gamma_{SL}\) - solid-liquid interfacial tension \([\frac{N}{m}\)],
\(\gamma_{LG}\) - liquid-vapor interfacial tension \([\frac{N}{m}\)].
The effect of different contact angles is presented in Figure 2:
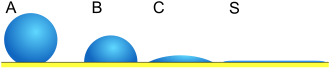
Wetting behavior varies between the fluids: in A, wetting is minimal with a large contact angle, whereas in C, wetting is greater with a small contact angle.
The contact angle matters in multiphase simulations because of several reasons:
- Sets interface orientation at walls: the contact angle prescribes how the interface meets solid boundaries, directly affecting local geometry used by Volume of Fluid method,
- Controls capillary forces and pressure: curvature near the contact line depends on the prescribed angle, so capillary pressure, Laplace forces, and resulting flows are sensitive to the contact angle,
- Affects dynamic contact-line behaviour: spreading, pinning, dewetting, and roll‑off behaviours require correct representation of advancing/receding angles or models for hysteresis to reproduce realistic dynamics,
- Influences macroscopic outcomes: wetting patterns in microfluidics, film deposition, breakup, and two‑phase flow in porous media are all controlled by boundary wetting conditions specified via the contact angle.
Constant Contact Angle provides a fixed contact angle value on the patch:
and the boundary alpha is adjusted according to the two-phase interface orientation consistent with this constant contact angle.
In some scenarios, the Zero Gradient boundary condition might be used - for example when the surface tension effects needs to be ignored. But it is important to note the consequences of such a decision:
- Zero Gradient prescribes that the wall normal gradient of alpha is zero, which does not impose any specific interface orientation or contact angle at the wall and therefore generally lets the interface meet the wall with whatever angle the volumetric solution produces, not the physical contact angle you want to enforce.
- Volume of Dluid (VoF) interface reconstruction and curvature evaluation rely on a correct wall boundary condition for alpha or for the contact‑angle field; without an explicit contact‑angle treatment the reconstructed interface and resulting capillary forces near the wall will be inconsistent with the intended wetting behaviour.
- Using Zero Gradient instead of a contact‑angle boundary condition typically produces spurious interface shapes, incorrect capillary pressure, and different dynamic contact‑line motion compared with a model that enforces the contact angle.
Constant Contact Angle - Boundary Condition Application & Physical Interpretation
The Constant Contact Angle boundary condition prescribes a fixed equilibrium contact angle for the phase volume-fraction field at a solid boundary, controlling how the interface meets the wall. It is used to model static wetting behavior where the contact angle between two phases and a solid surface is known and does not change dynamically. Its physical interpretation depends on the solver and the multiphase model: for VoF/VOF-like methods (e.g., interFoam (solver)) it enforces the interface curvature near the wall through the alpha field. For Eulerian multiphase solvers it constrains the phase distribution adjacent to solid surfaces.
Constant Contact Angle in Surface Wetting and Droplet Dynamics
Example applications: droplet spreading and impact, sessile drop equilibrium, contact-line pinning studies
These simulations are commonly solved with interFoam (solver) or other VoF-based solvers that capture sharp interfaces between immiscible fluids. The Constant Contact Angle boundary condition is applied on solid walls where the equilibrium (static) contact angle is known from experiment or material data, so the simulated interface meets the wall at that prescribed angle. This yields realistic static shapes for sessile drops, and can improve agreement with experiments when studying spreading, relaxation, or pinning on patterned surfaces.
| Physics | alpha (phase fraction) | Velocity |
|---|---|---|
Wall with known wettability | Constant Contact Angle | No-slip |
Constant Contact Angle in Coating, Printing, and Microfluidics
Example applications: film coating, inkjet drop deposition, microchannel flows with wetting
These problems involve thin liquid films and moving contact lines where the wall contact angle strongly affects film stability and deposition patterns. Using Constant Contact Angle at solid boundaries sets the local interface orientation independent of local flow-induced angle changes, which is useful for isolating the effect of substrate wettability in parametric studies. In microfluidic devices it helps reproduce controlled wetting conditions for capillary-driven flows and passive pumping.
| Physics | alpha | Velocity |
|---|---|---|
Coated substrate | Constant Contact Angle | No-slip or prescribed wall velocity |
Constant Contact Angle in Porous Media and Capillary Rise
Example applications: capillary imbibition into porous media, wick performance, oil-water displacement in channels
These simulations often use VoF or volume-fraction-based multiphase solvers to capture menisci in narrow geometries. Applying the boundary condition at solid boundaries prescribes the meniscus contact angle, controlling capillary pressure and penetration rates. This is important for predicting capillary-driven flows, retention in porous structures, and displacement efficiency in two-phase flows.
| Physics | alpha | Velocity |
|---|---|---|
Channel wall / pore surface | Constant Contact Angle | Zero Gradient or slip/no-slip depending on model |
Constant Contact Angle - Boundary Condition Constant Contact Angle in SimFlow
In SimFlow, the Constant Contact Angle boundary condition is applied to the alpha field (volume fraction) on wall patches in multiphase simulations. To use it, select the boundary condition type as Constant Contact Angle in the boundary conditions panel for the alpha field from the drop-down menu - Figure 3.
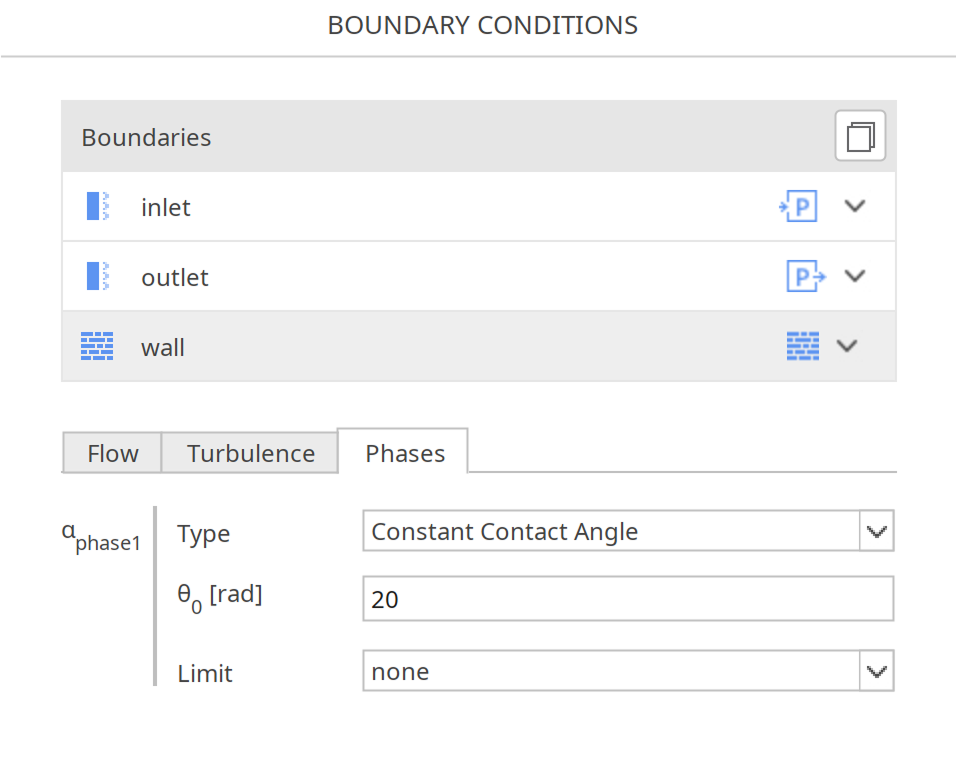
Specify the equilibrium contact angle and limit parameter:
\(\theta_0\) - contact angle \([\deg]\) (e.g., 90 for neutral wetting).
Limit - controls gradient behavior near the wall (e.g., gradient limiting for stability).
This ensures accurate interface orientation and capillary effects in solvers like interFoam equivalents.
Constant Contact Angle - Boundary Condition Constant Contact Angle - Alternatives
In this section, we propose boundary conditions that are alternative to Constant Contact Angle. While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
imposes a prescribed alpha value at the wall, useful when the exact phase fraction adjacent to the wall is known or when enforcing complete wetting/non-wetting | |
lets the phase fraction be extrapolated from the interior, suitable when the contact angle is not prescribed or when the wall influence should be minimal |