Heat Flux - Boundary Condition Description
Heat Flux boundary condition is applicable in the scenarios where the temperature of a wall is influenced by external heat flux. The boundary condition is particularly relevant in simulations involving conjugate heat transfer or where the heat flux at a boundary is a critical aspect of the simulation.
Heat Flux does not prescribe the wall temperature directly. Instead, it imposes a heat flux, and the wall temperature is obtained from the solution of the energy equation.
Heat Flux - Boundary Condition Understanding Heat Flux
The formula used in the calculations is the following:
\(q_n = \vec n \cdot q = - \kappa \nabla_n T\)
where:
- \(q_n\) - heat flux normal to the boundary \([\frac{W}{m^2}]\),
- \(\kappa\) - thermal conductivity defined in material properties \([\frac{W}{mK}]\),
- \(\nabla_n T\) - temperature gradient normal to the boundary \([\frac{K}{m}]\).
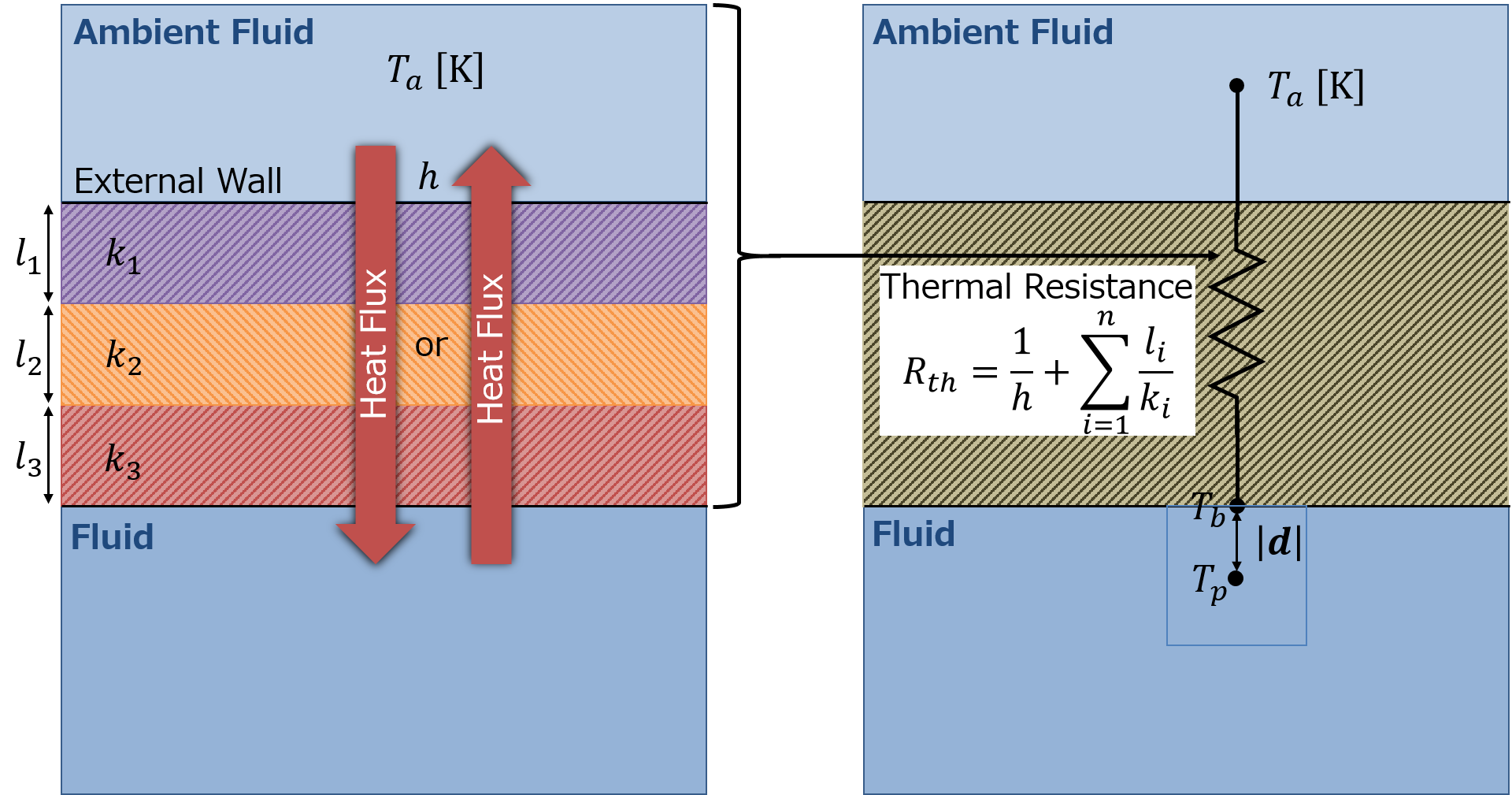
Additionally, the concept of thermal resistance, which is an analogue to electrical resistance in Ohm’s Law, can be introduced. The higher the thermal resistance, the lower the heat transfer through the material.
In the thermal-resistance analogy, the heat flux is related to the temperature difference across the wall by:
\(q_n = \frac{\Delta T}{R}\)
where:
- \(R\) is thermal resistance.
The total thermal resistance includes both conductive and convective components and can be expressed as:
\(R = \frac{1}{h} + \sum \frac{\delta_i}{\kappa_i}\)
where:
- \(h\) - heat transfer coefficient \([\frac{W}{m^2K}]\),
- \(\delta_i\) - thickness of the wall or its part,
- \(\kappa_i\) - thermal conductivity of the wall or its part \([\frac{W}{mK}]\).
This formulation represents a simplified one-dimensional thermal resistance model commonly used for interpretation of wall heat transfer.
Graphically, the above formula can be expressed as in Figure 1:
Heat Flux - Boundary Condition Application & Physical Interpretation
The Heat Flux boundary condition physically means that the boundary effectively represents the external thermal environment (flux, convection, radiation) and supplies the correct temperature or gradient so that the interior solution exchanges exactly that amount of heat.
Heat Flux in Thermal Analysis applications
Example applications: heat transfer through the wall
These types of simulations can be solved using the buoyantSimpleFoam (solver). This could involve studying the effectiveness of insulation or the impact of solar radiation on external walls.
The boundary condition is used to model the heat flux through building walls due to external factors like solar radiation, internal heating or cooling, and convective heat transfer with the external environment.
| Physics | Pressure | Velocity | Temperature |
|---|---|---|---|
Building’s wall | Zero Gradient | Fixed Value | Heat Flux |
Heat Flux - Boundary Condition Heat Flux in SimFlow
To define Heat Flux in SimFlow the proper option must be selected from the drop-down menu for the Wall boundary - Figure 2.
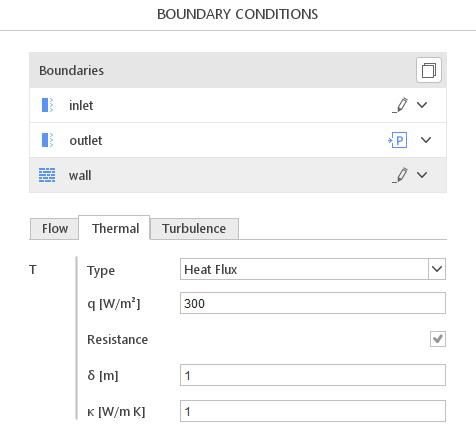
q - heat flux at the boundary
\(\delta\) - thickness of the wall
\(\kappa\) - thermal conductivity
Heat Flux - Boundary Condition Heat Flux - Alternatives
In this section, we propose boundary conditions that are alternative to Heat Flux. While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
fixes the temperature at the wall boundary | |
works in a similar way to Heat Flux, but Power \(P\) instead is defined | |
works in a similar way to Heat Flux, but Wall Heat Transfer coefficient \(h\) and ambient temperature \(T_{\infty}\) are defined |