Hydrostatic Pressure - Boundary Condition Description
Hydrostatic Pressure is a fixed-value boundary condition for the field \(p \_rgh\) - the “reduced-gravity” pressure that many buoyant and multiphase solvers solve instead of the raw static pressure p. The boundary condition is designed for cases where there is a hydrostatic pressure variation in the flow due to gravitational effects, particularly for buoyant and multiphase flows.
In many problems where hydrostatic pressure contribution \(\rho g h\) is important, in the momentum equation, the static pressure \(p\) is replaced with the modified pressure \(p \_rgh = p - \rho g h\).
This formulation ensures that the static pressure \(p\) is adjusted for the hydrostatic head, represented by \(\rho \vec g h\), which is the pressure increase due to the weight of the fluid column above the point in question.
Typical applications of Hydrostatic Pressure are:
- Open boundaries in free-surface (VOF) flows,
- Compressible buoyant or fire-driven flows,
- Hydraulic-head / open-channel problems
- HVAC
Hydrostatic Pressure - Boundary Condition Understanding Hydrostatic Pressure
Mathematically, Hydrostatic Pressure can be expressed as:
- \(p \_ \rho g h\) – the pseudo hydrostatic pressure \([Pa]\)
- \(p\) - static pressure \(Pa\),
- \(\rho\) – density,
- \(g\) – gravity vector,
- \(h\) – height in the opposite direction to gravity,
- \(h_{ref}\) – reference height in the opposite direction to gravity.
The reason why \(p \_ \rho gh\) term is used is driven by several factors:
- numerical conditioning - the hydrostatic term \(\rho g h\) can be orders of magnitude larger than the dynamic pressure variations that really matter to the flow. Removing it shrinks the range of numbers being solved for, so the Poisson matrix is far better conditioned and round-off error is reduced. Convergence is noticeably faster and more robust, especially for tall domains or high-density fluids
- cleaner momentum equation - in the Navier–Stokes momentum equation the gravity term and the hydrostatic part of \(\nabla p\) cancel exactly. Writing the equation in terms of p_rgh makes that cancellation explicit, leaving only the buoyancy contribution due to density differences \(\nabla (\rho) g\). This isolates the true driving force of natural-convection flows.
- straight-forward boundary conditions - many real boundaries are specified by a known static pressure (e.g. 0 Pa gauge at an opening). With p_rgh, users can still impose that familiar static value through the prghPressure BC, which converts it automatically at every face, accounting for local height and changing density. You don’t have to hand-build a tricky, height-dependent profile yourself
Hydrostatic Pressure - Boundary Condition Application & Physical Interpretation
Hydrostatic Pressure is typically used for pressure fields in solvers that separate the hydrostatic pressure from the dynamic pressure—commonly in buoyancy-driven flows (e.g., natural convection) and multiphase flows.
Hydrostatic Pressure in HVAC applications
Example applications: room cooling and heating
The buoyantPimpleFoam (solver) can be used for room cooling and heating simulations.
| Physics | Modified Pressure | Velocity | T |
|---|---|---|---|
Inlet | Fixed-Flux Pressure | Fixed Value | Fixed Value |
Outlet | Hydrostatic Pressure | Pressure Inlet-Outlet Velocity | Zero Gradient |
Hydrostatic Pressure - Boundary Condition Hydrostatic Pressure in SimFlow
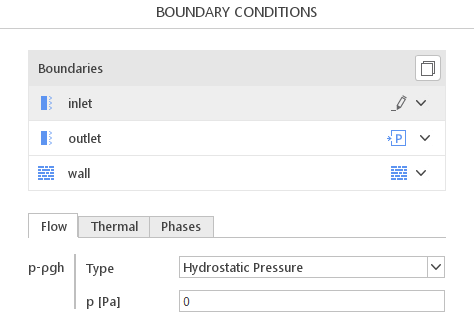
The definition of boundary conditions in SimFlow is both simple and intuitive. To specify the Hydrostatic Pressure boundary condition, the User must navigate to the Boundary Conditions panel, select the appropriate boundary for the pressure, and choose the correct option from the drop-down menu - Figure 1.
Hydrostatic Pressure - Boundary Condition Hydrostatic Pressure - Alternatives
In this section, we propose boundary conditions that are alternative to Hydrostatic Pressure. While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
defines total pressure condition for \(p \_ \rho g h\) | |
defines total pressure condition at the boundary | |
defines static pressure condition at the boundary |