Low Re Wall Function (k) - Boundary Condition Description
Low Re Wall Function (k) is a boundary condition that provides a wall constraint on the turbulent kinetic energy \(k\) for low- and high-Reynolds number turbulence models. This wall function distinguishes between the viscous sublayer and the inertial sublayer. From a user’s perspective, it adjusts the turbulent kinetic energy \(k\) based on the dimensionless wall distance \(y^+\), which depends on the height of the first cell adjacent to the wall. Low Re Wall Function (k) inherits from Fixed Value.
It should be noted that the term 'Low Reynolds' does not refer to the overall flow Reynolds number, but rather to the near-wall region where viscous effects dominate. In CFD practice, this implies that the near-wall region is well resolved with a sufficiently fine mesh (\(y^+ ≈ 1\)), so conventional wall-function modeling is not required. Conversely, the “High Reynolds” term applies when the mesh near the wall is not fine enough to resolve the viscous sublayer, thus requiring wall functions for accurate prediction of turbulent properties.
Low Re Wall Function (k) - Boundary Condition Understanding Low Re Wall Function (k)
The first step of prescribing the turbulent kinetic energy is to calculate estimated intersection of the viscous and inertial sublayers in wall units \(y_{lam}^+\)
- \(\kappa\) - von Kármán Constant \([-]\)
- \(E\) - Wall Roughness Parameter \([-]\)
The turbulent kinetic energy \(k\) is calculated based on the dimensionless wall distance \(y^+\), as described below.
The model expressions for \(k\) for viscous and inertial sublayers are switched in a stepwise manner:
\(k = k_{log} \quad\) if \(\quad y^+ > y_{lam}^+\)
\(k = k_{vis} \quad\) if \(\quad y^+ <= y_{lam}^+\)
- \(k_{vis}\) - \(k\) prediction in the viscous sublayer
- \(k_{log}\) - \(k\) prediction in the inertial sublayer
- \(y^+\) - estimated wall-normal height of the cell center in wall units
- \(y_{lam}^+\) - estimated intersection point of the viscous and inertial sublayers in wall units
Additional equations:
- \(C_k\), \(B_k\), \(C_{\mu}\), \(\kappa\) - model constants
- \(u_{\tau}\) - friction velocity
- \(y\) - wall-normal height
- \(\nu_w\) - kinematic viscosity near the wall
It is important to note that while Low Re Wall Function (k) can prescribe \(k\) when the first cell is located in the buffer layer, it is generally recommended to avoid placing the center of the first cell in this region for improved accuracy.
Low Re Wall Function (k) - Boundary Condition Application & Physical Interpretation
Low Re Wall Function (k) is crucial for accurately simulating turbulent flows, such as development of boundary layer on surfaces, pipe or channel flows, and turbulent flows over a bump (geometrical features) that cause flow separation.
Low Re Wall Function (k) in Channel and Pipe Flow applications
Example applications: pipe or duct flow
These types of simulations can be solved using the pimpleFoam (solver).
| Physics | Pressure | Velocity | \(k\) | \(\epsilon\) | \(nu_t\) |
|---|---|---|---|---|---|
Pipe (Wall) | Zero Gradient | No-Slip | Low Re Wall Function (k) | Fixed Value | Low Re Wall Function |
Low Re Wall Function (k) - Boundary Condition Low Re Wall Function (k) in SimFlow
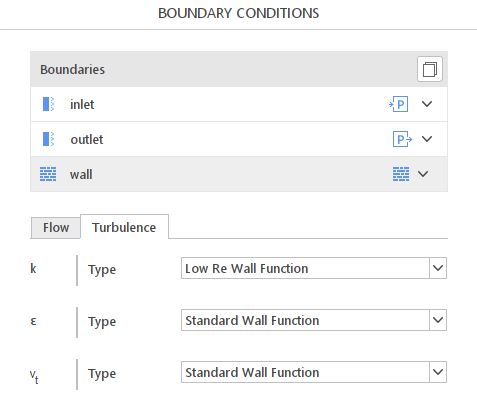
To define Low Re Wall Function (k), the proper option must be selected from the drop-down menu for the turbulent kinetic energy \(k \)- Figure 1. No further input is required.
Low Re Wall Function (k) - Boundary Condition Low Re Wall Function (k) - Alternatives
In this section, we propose boundary conditions that are alternative to Low Re Wall Function (k). While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
fixed value on the patch | |
prescribes turbulent kinetic energy \(k\) for high-Reynolds conditions |