Moving Wall Velocity - Boundary Condition Description
Moving Wall Velocity is a wall‑type velocity boundary condition for moving‑mesh cases. It enforces the no‑slip condition in the wall’s own frame by setting the fluid velocity on the patch equal to the instantaneous mesh (wall) velocity each time step. Hence, the relative velocity between the fluid and the wall is always zero.
The value entry you supply in the dictionary is only an initial guess; it is overwritten as soon as the simulation advances. Consequently:
- the user does not have to prescribe a non‑zero value to “drag” the fluid: the condition automatically pulls the fluid along with the wall motion, and
- if a non‑zero relative velocity between fluid and wall is needed, a different boundary condition must be used (e.g. Fixed Value in combination with the appropriate mesh motion), as Moving Wall Velocity will always impose the wall velocity itself.
Moving Wall Velocity - Boundary Condition Understanding Moving Wall Velocity
Moving Wall Velocity is a boundary condition used to simulate the movement of a wall in a fluid domain. It is primarily used in problems where the wall or boundary is not stationary and is moving with a certain velocity. It imposes the local velocity of the wall as calculated from the mesh motion on the adjoining fluid cell faces, so the fluid sticks to (and convects with) any translating, rotating or deforming wall. In other words, Moving Wall Velocity works for a moving wall, as No-Slip for a stationary wall.
Mathematically, Moving Wall Velocity can be expressed by the following formula:
- \(U_{p}\) - velocity on the wall face
- \(\vec n\) – unit outward face normal
- \(U_{mesh}\) – mesh (wall) velocity at the face center
- \(U_n\) - normal component of the interior‑cell velocity, \(\vec U \cdot \vec n\)
- \(U_{mesh} = \frac{x_{new} – x_{old}}{\Delta t}\) – ensures normal flux continuity and zero tangential slip
- \(\Delta t\) – time step size
- \(x_{new}, x_{old}\) – new and old mesh position
The mesh velocity is obtained every time step from the vertex displacements. The term \( \vec n (U_n – \vec n \cdot U_{mesh})\) corrects the normal component so that the relative mass flux is exactly zero, keeping the wall impermeable even while the mesh moves. Moving Wall Velocity only works on patches defined as wall boundary.
Moving Wall Velocity - Boundary Condition Application & Physical Interpretation
Moving Wall Velocity is tailored for prescribing velocity on moving walls. It finds applications in CFD simulations related to pumps, fans and rotor simulations, or sliding and overset meshes.
Moving Wall Velocity in VoF (Volume of Fluid) applications
Example applications: ship hull calculations, sloshing, ship hydrodynamics
This problem can be addressed using the interFoam (solver). Moving Wall Velocity is applied at the walls of the moving object.
| Physics | Pressure | Velocity | Phases \(\alpha\) |
|---|---|---|---|
Hull | Fixed Flux Pressure | Moving Wall Velocity | Zero Gradient |
| Tutorial | Description |
|---|---|
Multiphase simulation with dynamic mesh representing the rotating impeller in a cylindrical tank. |
Moving Wall Velocity in Rotating Machinery applications
Example applications: propellers
This problem can be addressed using the pimpleFoam (solver). Moving Wall Velocity is applied at the walls of the rotating object.
| Physics | Pressure | Velocity |
|---|---|---|
Propeller | Zero Gradient | Moving Wall Velocity |
Moving Wall Velocity - Boundary Condition Moving Wall Velocity in SimFlow
To define Moving Wall Velocity boundary condition on the patch, the proper option must be selected from the drop-down menu in Boundary Conditions tab - Figure 1.
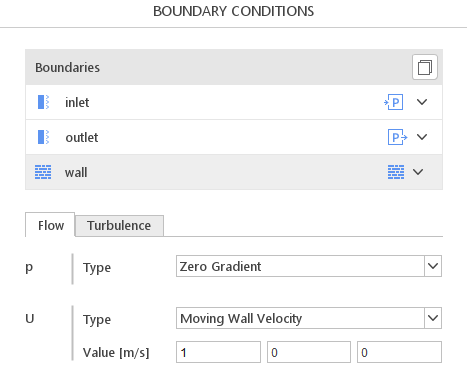
Once selected, the user can enter the initial value of the velocity. It should be remembered that the provided value of the initial velocity will be overwritten by solver during calculations - the velocity of the moving fluid will be reassigned.
- \(Value \ [m/s]\) - initial value of the moving wall velocity
Moving Wall Velocity - Boundary Condition Moving Wall Velocity - Alternatives
In this section, we propose boundary conditions that are alternative to Moving Wall Velocity. While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
defines zero relative velocity between fluid and the stationary wall | |
works exactly in the same way as Moving Wall Velocity but for the rotating walls |