Rough Wall Function - Boundary Condition Description
Rough Wall Function specifies the turbulent kinematic viscosity \(\nu_t\) when applying wall functions for rough surfaces, with a focus on velocity-based calculations. Wall functions are utilized to model turbulence within the boundary layer, particularly near the wall region. In typical flows, the velocity at the wall is always set to zero. However, resolving the actual roughness at the wall is impractical due to its small scale and the high computational cost involved. Consequently, turbulent viscosity must be modeled artificially to account for these effects.
The function works by adjusting the kinematic eddy viscosity based on roughness parameters, effectively changing the turbulence model’s behavior near the wall. Unlike nutkRoughWallFunction (k-based) or nutUSpaldingWallFunction (smooth walls), this BC uses velocity-based calculations for rough surfaces.
Rough Wall Function - Boundary Condition Understanding Rough Wall Function
Rough Wall Function imposes a wall constraint on the turbulent viscosity \(\nu_t\) based on the velocity (U) for both low- and high-Reynolds number turbulence models in the presence of rough walls. Velocity-based formulation means that the condition works with turbulence models which do not calculate explicitly turbulent kinetic energy \(k\) (for example \(k-\epsilon\) or \(k-\omega\)). An example of such a turbulence model is the Spalart-Allmaras model.
The turbulent viscosity \(\nu_t\) is calculated according to the following formulas:
\(\nu_t = 0\) if \(y^+ <= y_{lam}^+\)
\(\nu_t = \nu_w ( \frac{ (y^+)^2}{Re} -1) \quad\) if \(\quad y^+ > y_{lam}^+\)
with
\(Re = \frac{u_py}{\nu_w}\)
- \(\nu_t\) - turbulent viscosity \([m^2/s]\)
- \(Re\) - Reynolds number \([-]\)
- \(\nu_w\) - kinematic viscosity of fluid near wall \([m^2/s]\)
- \(y^+\) - Estimated wall-normal height of the cell center in wall units
- \(u_p\) - velocity in the cell center near the wall \([m/s]\)
- \(y\) - distance from the wall to the cell center \([m]\)
Rough Wall Function - Boundary Condition Application & Physical Interpretation
Rough Wall Function is crucial for accurately simulating flows over rough surfaces in turbulent conditions. By adjusting the kinematic eddy viscosity based on surface roughness, it allows for a more realistic representation of wall effects in CFD models. This is particularly important in engineering applications such as pipelines, ducts, and channels where wall roughness plays a significant role in flow behavior.
Rough Wall Function in Pipe Flow applications
Example applications: pipe or duct flow
These types of simulations can be solved using the simpleFoam (solver). In this case, we assume that the inner surface of the pipe is not perfectly smooth, but rather is characterized by some roughness.
| Physics | Pressure | Velocity | \(nu_{SA}\) | \(nu_t\) |
|---|---|---|---|---|
Pipe (Wall) | Zero Gradient | No-Slip | Zero Gradient | Rough Wall Function |
Rough Wall Function - Boundary Condition Rough Wall Function in SimFlow
To define Rough Wall Function on the wall boundary, switch the turbulent viscosity parameter (\(\nu_t\)) from Standard Wall Function to Rough Wall in the Turbulence tab - Figure 1. Note that turbulence fields are available only if a RANS turbulence model is selected. The laminar model does not simulate any turbulence effects.
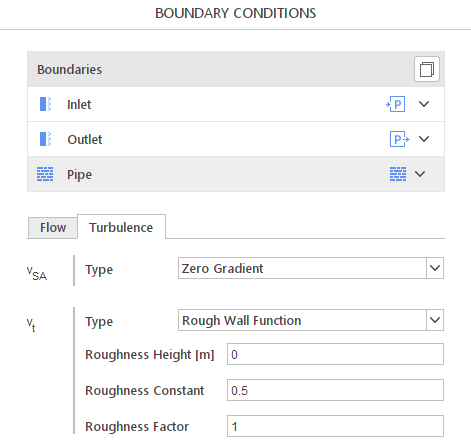
- Roughness Height - represents the equivalent sand grain roughness height in \([m]\)
- Roughness Constant - Dimensionless constant that characterizes the type of roughness; default is 0.5
- Roughness Factor - Scaling factor; nominally = 1
Rough Wall Function - Boundary Condition Rough Wall Function - Alternatives
In this section, we propose boundary conditions that are alternative to Rough Wall Function. While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
fixed value on the patch | |
similar to Rough Wall Function but calculates \(nu_t\) based on turbulent kinetic energy |