Total Pressure - Boundary Condition Description
Total Pressure boundary condition fixes the static pressure on the domain boundary based on a specification of the total pressure \(p_{0}\). In many cases, Total Pressure is recommended due to the stability reasons. The boundary condition works differently depending on the flow regime: incompressible, subsonic compressible and supersonic compressible flows.
If one wants to define the pressure driven flow, setting the static pressure by Fixed Value boundary condition may lead to instability of the solver because of fixed pressure gradient, which constantly accelerates the flow.
Total Pressure - Boundary Condition Understanding Total Pressure
Total Pressure is applicable for both incompressible and compressible flows, though the total pressure definition is expressed in a different manner depending on the flow type.
Incompressible flows
For incompressible flows, the density of the fluid is assumed to be constant. Therefore, Total Pressure is typically applied at the inlet and outlet boundaries of the domain. This condition allows the solver to determine the velocity field consistent with the prescribed total pressure and boundary conditions.
Mathematically, Total Pressure can be expressed as:
- \(p_{s}\) - static pressure
- \(p_{0}\) - total pressure
Based on the above formula, the velocity \(U\) can be easily calculated as:
\(U = \sqrt{2(p_0-p)}\)
Please remember that for incompressible flows, the flux is expressed in \([m^3/s]\) and pressure is expressed in \([m^2/s^2]\) - the pressure is called the kinematic pressure.
Subsonic compressible
The pressure definition includes density and is expressed as below:
Transonic compressible
For transonic compressible flow, the relation between static and total pressure looks as follows:
- \(\psi\) - compressibility (for fixed composition of gas) expressed as \(\psi = (RT)^{-1}\)
- \(R\) - gas constant
- \(T\) - temperature
Supersonic compressible
Supersonic compressible flows are using 1D isentropic flow equation:
- \(\gamma = C_p/C_v\) - ratio of specific heats for a given fluid
Total Pressure - Boundary Condition Application & Physical Interpretation
Total Pressure is used for pressure-driven flows, where the velocity at the inlet is unknown. Instead, the total pressure (also called stagnation pressure) can be prescribed for both incompressible and compressible types of flow.
Total Pressure in Channel/Pipe Flow applications (Incompressible Flows)
Example applications: pipe flow
These types of simulations can be solved using the pimpleFoam (solver) This solver has two basic independent variables: pressure and velocity. Additionally, turbulence-related variables can be defined. Total Pressure can be applied to the domain inlet if the velocity is unknown.
| Physics | Pressure | Velocity |
|---|---|---|
Pressure Inlet | Total Pressure | Pressure Inlet Outlet Velocity |
Total Pressure in Multiphase applications
Example applications: free surface flows (free/entrainment boundaries), for example ship hull motion
The interFoam (solver) can be used for free surface modeling problems. When the free boundary exists in the domain, both inflow and outflow may occur on such a patch. zeroGradient for velocity and Fixed Value for pressure are not recommended as they may lead to instability. Instead, Total Pressure supports inflow and outflow through the boundary as well as improves the stability of the solution.
| Physics | Modified Pressure | Velocity |
|---|---|---|
Atmosphere | Total Pressure | Pressure Inlet Outlet Velocity |
Total Pressure in Combustion applications
Example applications: fire modelling in compartments, flame propagation
The reactingFoam (solver) can be used for flame propagation. To model stable flame behavior without risk of backflows, it is recommended to apply Total Pressure at the outlet.
| Physics | Pressure | Velocity | Temperature |
|---|---|---|---|
Outlet | Total Pressure | Pressure Inlet Outlet Velocity | Inlet Outlet |
Total Pressure - Boundary Condition Total Pressure in SimFlow
Incompressible flows
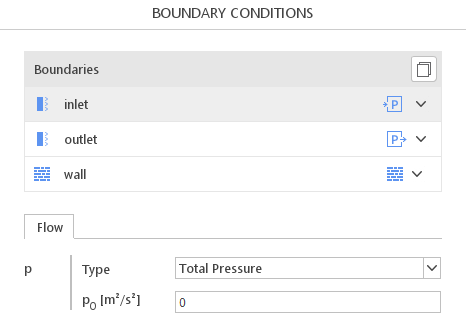
For incompressible flows, the only required parameter to be defined is total pressure \(p_{0}\). However, in SimFlow, all incompressible solvers are using pressure divided by density. Such pressure is called the kinematic pressure and is expressed in \(m^2/s^2\) - Figure 1
Compressible flows
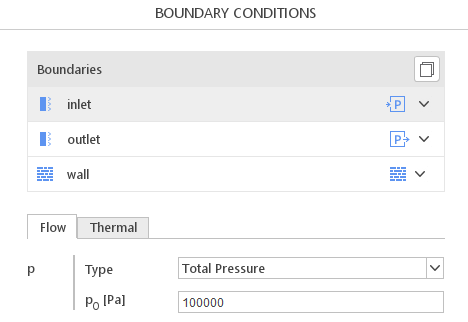
For compressible flows, the required parameter is total pressure \(p_{0}\) expressed in \(Pa\). The density \(\rho\) and heat capacity \(c_{p}\) are taken from material properties defined in Thermo section - Figure 2.
Total Pressure - Boundary Condition Total Pressure - Alternatives
In this section, we propose boundary conditions that are alternative to Total Pressure. While they may fulfill similar purposes, they might be better suited for a specific application and provide a better approximation of physical world conditions.
| Boundary Condition | Description |
|---|---|
similar boundary condition, but it allows to define time-dependent total pressure | |
the most basic boundary conditions, where the value of variable (like pressure) is fixed across the boundary. It is used in scenarios where the boundary value is known and constant (it defines static pressure). |