Cell Zones
Introduction
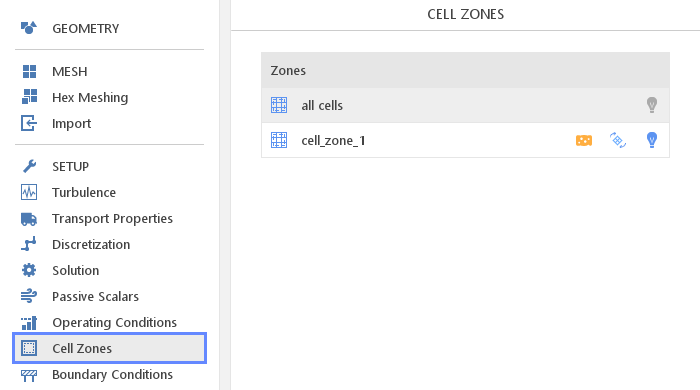
Most properties of the model defined in SimFlow are applied to the entire domain. However, it is often necessary to applied certain properties only at a specific location. Such models can be defined in the Cell Zones and assigned to a specific cell zone in the mesh.
Zonal Models:
Porosity
Multiple Reference Frames (MRF)
Source Terms
Editing Zonal Models
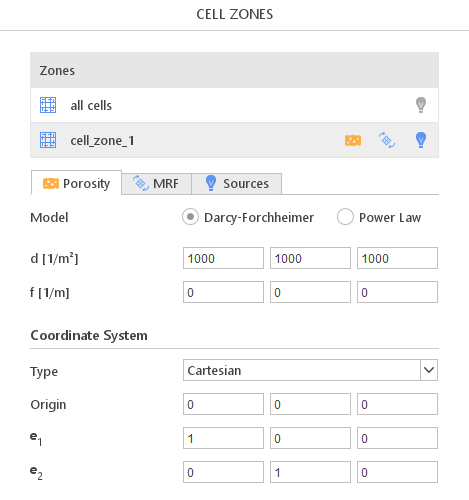
Properties of a given cell zone can be enabled or disabled by clicking on the appropriate icon to the right of the zone name. Panels for editing models are displayed below the list. The Zones list contains all user created cell zones as well as a virtual cell zone named all cells representing all cells in a given mesh region. The virtual zone can be used for the source term definition in the entire mesh region.
Porosity Modelling
Porosity models introduce additional resistance into the flow. They are used to model an object whose geometry is not very important or consists of very small structures that would be impossible to resolve (e.g. sand bed).
The user can choose between two models of porosity:
- Darcy-Forchheimer
- Power Law
Darcy-Forchheimer Model
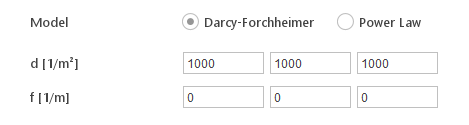
Darcy-Forchheimer law porosity model is given by:
\(S=-(\mu d+ \frac{\rho |\mathbf{U}|}{2}f)\mathbf{U}\)
where Darcy d and Forchheimer f coefficients need to be specified by the user. Note that these coefficients need to be specified in the local coordinate system.
Power Law Model
Power law porosity model is given by: \(S=-\rho C_0 |\mathbf{U}|^{(C_1-1)}\mathbf{U}\)
where \(C_0\) and \(C_1\) are model coefficients that need to be specified by the user.
Local Coordinate System
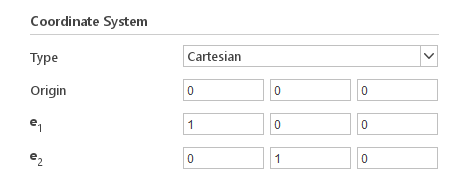
Certain porosity models allow for anisotropic porosity properties and require coefficients to be specified in a local coordinate system. For convenience the default local coordinate system is equivalent to the global coordinate system, which means that when porosity properties are aligned with the global coordinate system no additional inputs are required.
Coordinate System Options:
- Type - type of coordinate system
- Cartesian
- Cylindrical
- Origin - origin point of the local coordinate system
- \(e_1\) - first axis of the local coordinate system (X axis)
- \(e_2\) - second axis of the local coordinate system (Y axis)
Multiple Reference Frames Modelling
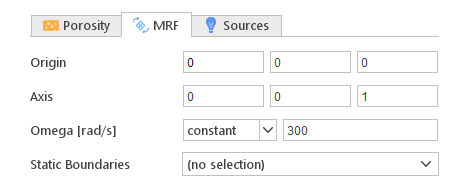
Modelling rotating elements like fans or blowers can be computationally expensive since it requires a transient simulation with moving mesh. However, it is often possible to use different reference frames for different parts of the flow, e.g. rotating frame for rotor and stationary frame for diffuser. This way in both frames we can solve steady state equations. This approach is only an approximation, but when there is no significant interactions between rotating and stationary boundaries, it can provide sufficient accuracy with relatively low computational cost.
Rotating Reference Frame Definition:
- Origin - center of rotation
- Axis - axis of rotation
- Omega - rotational speed
- Static Boundaries - list of boundaries that should be treated in stationary and not rotating frame
Source Term Modeling
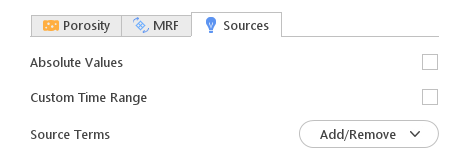
In certain situations, you need to define source terms for specific equations. A typical situation is to include an energy source that represents Joule heating.
Options:
- Absolute Values - specifies whether the source term is defined as absolute (e.g. \([W]\)) or per unit volume (e.g. \([W / m ^3 ]\))
- Custom Time Range - allows you to define start time and duration of the source term. If not specified the source term will be applied during entire simulation
- Source Terms - allows you to select equations for which to add source term and display source term options
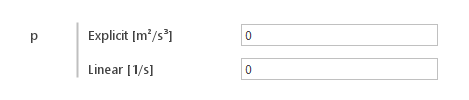
For each equation \(\Psi\) you can define source term explicitly \((S\Psi=A)\) or as a linear function of \(\Psi(S \Psi=B \cdot \Psi)\)
Source Term Definition:
- Explicit - explicit value of the source term (A)
- Linear - proportionality coefficient for the source term (B)