Discretization
Introduction
To calculate flow field it is required to solve the Navier-Stokes equations inside the flow domain. This is a system of partial differential equations which cannot be solved analytically in general and needs to be converted into a system of linear equations. The process of converting partial differential equation into a linear equation system is called discretization and can use multiple different schemes.
In the Discretization panel one selects discretization schemes that are most suitable for the given simulation type. Usually, when selecting discretization scheme there is a trade-off between accuracy and stability, which may require some testing to select optimal scheme.
Time Discretization
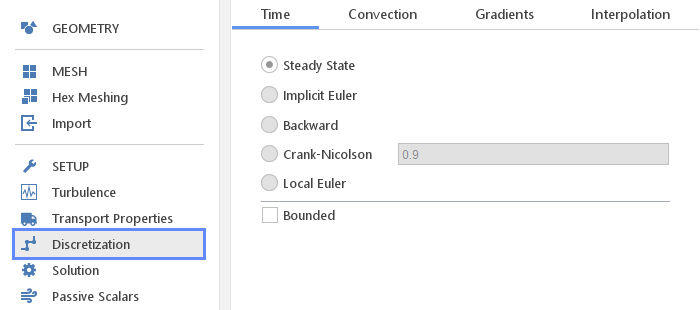
The Time discretization tab defines how terms of the form \(\frac{\partial\Psi}{\partial t}\) need to be discretized.
Time Discretization Schemes:
- Steady State - terms with temporal derivatives are not discretized, which is usually used in steady-state simulation
- Implicit Euler - basic Euler scheme (first-order), uses only the current and previous time-step values
- Crank-Nicolson - Crank-Nicolson scheme (second-order), requires specification of an "off-centering" coefficient (1 - pure Crank-Nicolson, 0 - pure Implicit Euler)
- Backward - backward-differencing scheme (second-order), uses the current and two previous time-step values
- Local Euler - local time-step Euler scheme (first-order), local time-step field is looked-up from the database. This scheme should only be used for steady-state computations using transient codes where local time-stepping is preferable to under-relaxation for transport consistency reasons.
- Bounded - option for selecting the bounded form of the underlying scheme. Boundedness is achieved by subtracting \(\frac{\partial \varphi}{\partial t} \cdot \Psi\) which is non-conservative if \(\frac{\partial \rho}{ \partial t} \neq 0\) but conservative otherwise.
Convection (Advection) Discretization
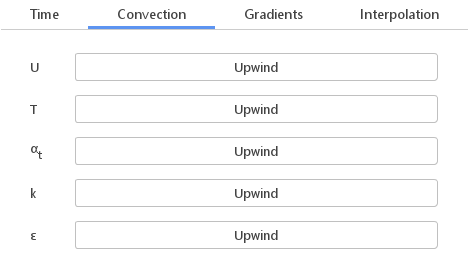
The Convection discretization tab defines how terms of the form \(\nabla \cdot(\vec U\cdot \Psi)\) need to be discretized. Since usually different equations require different treatment, one needs to define convection scheme for each individual equation.
Defining Convection Scheme
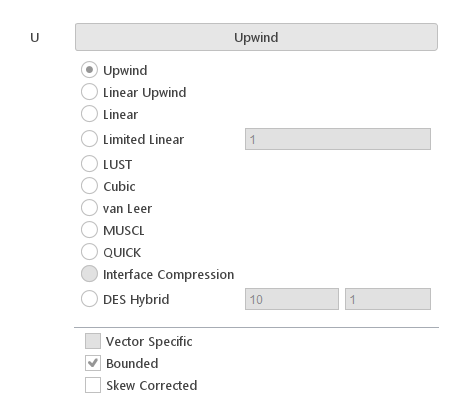
To specify convection scheme for a given field (for example velocity), one needs to click the button next to the name of the equation. This will cause a panel with available options to expand. When the new scheme is selected, the label of the button will change and display new scheme’s name.
Convection Schemes:
- Upwind - upwind differencing scheme (first-order, bounded)
- Linear Upwind - linear upwind differencing scheme (second-order), calculates upwind weighting factors and also applies a gradient-based explicit correction
- Linear - central-differencing scheme (second-order, unbounded)
- Limited Linear - TVD limited linear differencing scheme (second-order)
- LUST - linear-upwind stabilised transport scheme (second-order), blended linear/linear-upwind scheme For this discretization, velocity gradients need to be specified. This scheme is used for large eddy simulation (LES).
- Cubic - modified version of Linear scheme which applies an explicit correction (second-order)
- van Leer - discretization scheme with van Leer flux limiter (second-order)
- MUSCL - MUSCL differencing scheme (second-order)
- QUICK - quadratic-upwind differencing scheme (second-order)
- Interface Compression - modeled relative velocity used to compress the interface
- DES Hybrid - hybrid convection scheme for DES calculations. The scheme blends between a low-dissipative linear convection scheme within the LES region and a numerically more robust upwind scheme in the RAS region. It requires you to specify responsively velocity and length scales.
Convection Scheme Options:
- Vector Specific - this option enables special version of the scheme dedicated for discretization of vector fields
- Bounded - option for selecting bounded form of the underlying scheme. Boundedness is achieved by subtracting \((\nabla \cdot \rho U)\Psi\) which is non-conservative if \(\frac{\partial \rho}{ \partial t} \neq 0\) but conservative otherwise. Can be used for convection of bounded scalar properties in steady-state solvers to improve stability if insufficient convergence of the pressure equation causes temporary divergence of the flux field.
- Skew Corrected - skewness-corrected interpolation scheme that applies an explicit correction to an underlying scheme
Gradiend Discretization
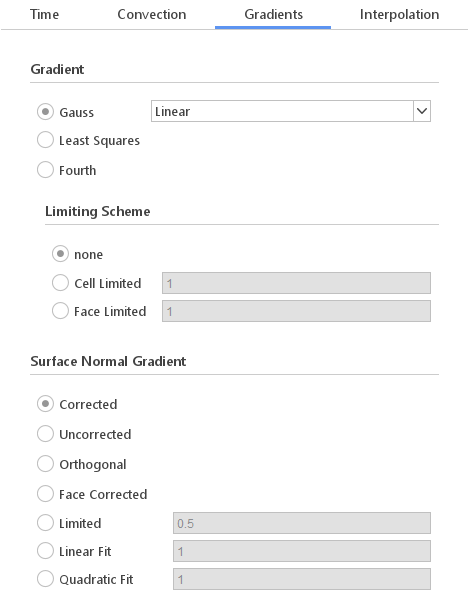
The Gradients tab defines discretization schemes used for calculating gradients.
Defining Gradient Scheme
The Gradient discretization scheme once selected is applied to all fields.
Gradient Schemes:
- Gauss - basic gradient scheme using face-interpolation and Gauss' theorem (second-order)
- Least Squares - gradient scheme using least-squares (second-order)
- Fourth - gradient scheme using least-squares (fourth-order)
Gradient Limiting Schemes:
- none - no limiting is applied
- Cell Limited - scalar limiter based on limiting the extrapolated face values between the maximum and minimum cell and cell neighbour values and is applied to all components of the gradient
- Face Limited - scalar limiter based on limiting the extrapolated face values between the face-neighbour cell values and is applied to all components of the gradient
Defining Surface Normal Gradient Scheme
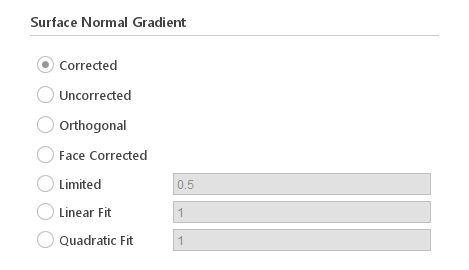
The Surface Normal Gradient once selected applies to all fields also when calculating the Laplace operator.
Surface Normal Gradient Schemes:
- Corrected - simple central-difference scheme with non-orthogonal correction
- Uncorrected - simple central-difference scheme without non-orthogonal correction
- Orthogonal - simple central-difference scheme without non-orthogonal correction
- Face Corrected - simple central-difference scheme with non-orthogonal correction
- Limited - scheme with limited non-orthogonal correction. The limiter is controlled by a coefficient with a value between 0 and 1 which when zero switches the limiter off and the scheme behaves as Corrected, and when set to 1 the limiter is calculated such that the non-orthogonal contribution does not exceed the orthogonal part.
- Linear Fit - centred fit scheme with linear polynomial and explicit correction
- Quadratic Fit - centred fit scheme with quadratic polynomial and explicit correction
Interpolation
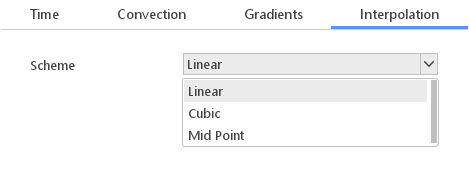
The Interpolation tab defines face interpolation scheme, which is going on be used. The selected scheme will also be used when calculating Laplace and divergence operators.
Interpolation Schemes:
- Linear - central-differencing interpolation
- Cubic - modified version of Linear scheme which applies an explicit correction
- Mid Point - mid-point interpolation (weighting factors = 0.5) scheme