Solution
Introduction
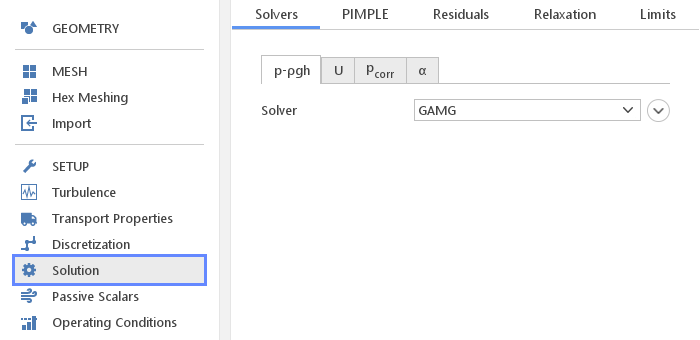
In the Solution panel you can define various aspects related to the actual solution process.
Linear Equations Solvers
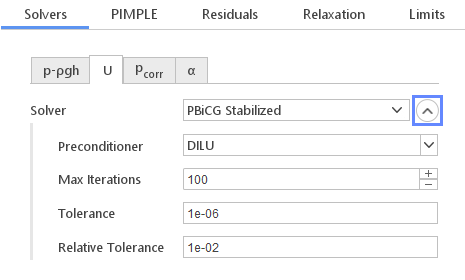
In the Solvers tab you have the possibility to define solver for each of the equations in the current simulations. Solver settings for each equation is put into separate tab. As usual all the default setting should be suitable for most general cases.
Available solvers in the Solver input depend on whether the matrix of a particular equation is symmetric or asymmetric. List of solvers can also change depending on the version of OpenFOAM that is currently being used.
Available Solvers:
- PCG - preconditioned conjugate gradient solver (symmetric only)
- PBiCG - preconditioned bi-conjugate gradient solver (asymmetric only)
- PBiCG Stabilized - preconditioned bi-conjugate gradient stabilized solver (asymmetric only)
- Smooth Solver - solver that in each iteration performs multiple smoother iterations
- GAMG - geometric agglomerated algebraic multigrid solver
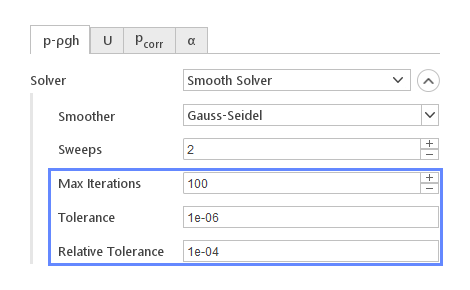
When you click the expand button detail solver settings will be displayed. Certain options, in particular that control the convergence are common for all the solvers.
Common Solver Options:
- Max Iterations - maximum number of iterations that the solver should perform. After this number of iterations is reached the solver will halt even if convergence criteria were not met.
- Tolerance - a residual level below which the equation system is considered solved.
- Relative Tolerance - residual level change ratio below which the equation system is considered solved even if the Tolerance level was not reached. If set to zero the relative tolerance is not considered.
Conjugate Gradient Solvers

PCG , PBiCG and PBiCGStab belong to the same family of solvers that use the conjugate gradient method . All solvers require specification of the preconditioning algorithm under the input Preconditioner . The list of available preconditioners will depend on whether the equation has a symmetric or asymmetric matrix.
Smooth Solver

Smooth Solver in each iteration performs multiple smoothing iterations using selected algorithm(e.g. Gauss-Seidel). For improved performance residual is evaluated after specified number of smoothing iterations.
Smooth Solver Specific Options:
- Smoother - smoothing algorithm
- Sweeps - number of smoother iterations per solver iteration
GAMG Solver
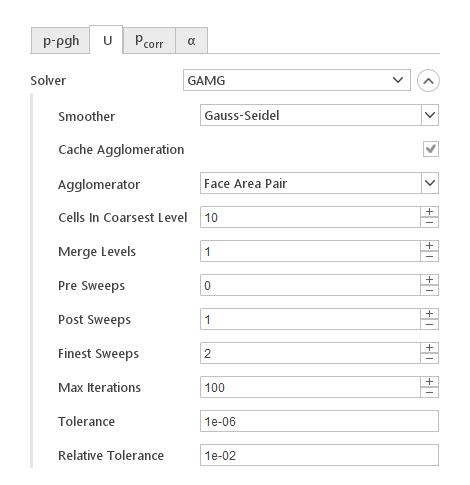
The GAMG solver is usually used for equations that are hard to converge, which is typically the pressure equation. For most other equations, especially in steady-state simulations, it can be too computationally expensive and other solvers should be used.
GAMG Specific Options:
- Smoother - smoothing algorithm
- Cache Agglomeration - option for enabling caching of the multigrid matrix hierarchy for improved efficiency
- Agglomerator - algorithm for agglomerating coarse matrix
- Cells In Coarsest Level - specifies how many equations (cells) should be in the coarsest matrix of the multigrid hierarchy
- Merge Levels - specifies how many standard matrix levels should be merged into the final level (controls the speed of coarsening of the levels). When set to 1 no merging is performed.
- Pre Sweeps - number of sweeps as the algorithm is coarsening
- Post Sweeps - number of sweeps as the algorithm is refining
- Finest Sweeps - number of sweeps at finest level
Preconditioners
Preconditioning algorithms are used by the conjugate gradient family of solvers to improve convergence rate of the solver.
Available Preconditioners:
- none - no preconditioning is applied
- diagonal - Jacobi preconditioner, uses inverse of the diagonal of the original matrix
- DIC - simplified diagonal-based incomplete Cholesky preconditioner (symmetric only)
- DILU - simplified diagonal-based incomplete LU preconditioner (asymmetric only)
Smoothers
Smoothing algorithms are used by GAMG and Smooth Solver.
Available Smoothers:
- Gauss-Seidel - smoother performing an iteration of the Gauss-Seidel method
- DIC - simplified diagonal-based incomplete Cholesky smoother (symmetric only)
- DILU - simplified diagonal-based incomplete LU smoother (asymmetric only)
- DIC & Gauss-Seidel - smoother performing DIC & Gauss-Seidel iterations
- DILU & Gauss-Seidel - smoother performing DILU & Gauss-Seidel iterations
Phase Fraction Solvers
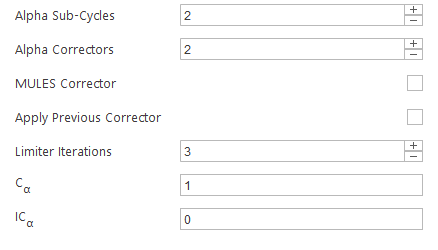
Solver used for calculating phase fraction \(\alpha\) in multiphase simulations have certain additional options besides the specification of the linear solver.
Options:
- Alpha Sub-Cycles - number of sub-cycles when solving \(\alpha\) equation
- Alpha Correctors - number of \(\alpha\) corrector iterations
- MULES Corrector - enable MULES algorithm correction
- Apply Previous Corrector - apply compression correction from the previous iteration
- Limiter Iterations - number of MULES limiter iterations
- \(C_\alpha\) - flux compression coefficient
- \(IC_\alpha\) - isotropic compression coefficient
Solution Schemes
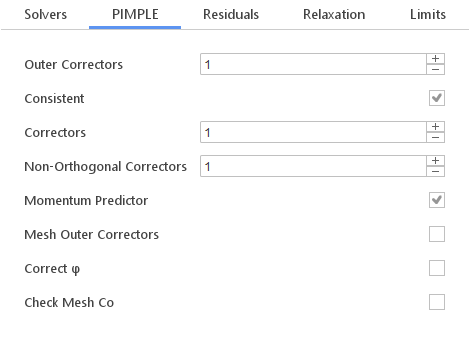
For solution of most fluid dynamic problems SimFlow uses either the Pressure-Implicit with Splitting of Operator ( PISO ), the Semi-Implicit Method for Pressure Linked Equations ( SIMPLE ) algorithms, or a combined PIMPLE algorithm. These algorithms are iterative procedures for coupling equations for momentum and mass conservation, PISO and PIMPLE being used for transient problems and SIMPLE for steady-state.
Options for current solution algorithms are displayed in a tab with a name of the algorithm.
General Scheme Options:
- Consistent - enables consistent formulation of the SIMPLE algorithm. With this option enabled relaxation factors can be increased which in turn increases the convergence rate.
- Outer Correctors - specifies the number of times the entire system of equations is solved within one time step
- Correctors - specifies the number of times the algorithm solves the pressure equation and momentum corrector in each iteration
- Non-Orthogonal Correctors - specifies number of times the pressure equation is solved the explicit non-orthogonal correction
- Momentum Predictor - enables the momentum predictor stage of the algorithm. Disabling momentum predictor can sometimes increase stability of the simulation.
- Mesh Outer Correctors -
- Correct \(\varphi\) -
- Check Mesh Co -
Residual Control

In the Residual tab you can modify the convergence criteria for each of the equations being solved under current settings. The equation is considered convergent if the normalized residual level drops below the specified value. The entire simulation is considered convergent if all equations converged.
Relaxation Factors
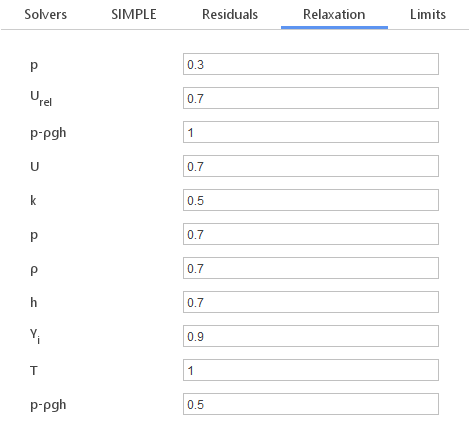
A technique called under-relaxation is used to increase the stability of steady state simulation. Under-relaxation works by limiting the amount which a variable changes from one iteration to the next, either by modifying the solution matrix and source prior to solving for a field or by modifying the field directly. In the Relaxation tab you can modify the default values of relaxation factors for each field or equation.
Limits
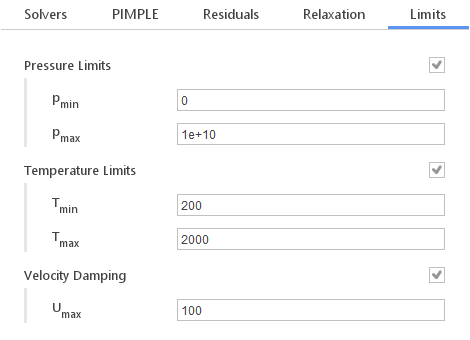
In the Limits tab you can apply limits on values of certain solution variable. By applying this limits you can increase the stability of the simulation, especially in the initial iterations. Be careful to specify limits in such a way that they are outside the solution range to avoid artificial variable value cutoff caused by the limits.
Available limiting options strongly depend on currently selected solver and the version of OpenFOAM being used. In certain situations, the Limits tab might even be unavailable.
Limiting Options:
- Pressure Limits - allows you to bound pressure between \(p_{min}\) and \(p_{max}\)
- Temperature Limits - allows you to bound temperature between \(T_{min}\) and \(T_{max}\)
- Velocity Damping - allows you to keep velocity below the specified \(U_{max}\) value